LOG (ROM-Routine)

Aus C64-Wiki
Zur Navigation springenZur Suche springen

Anmerkung: Dieser Artikel beschreibt die numerische LOG-Routine im BASIC-ROM.

Name: LOG
Beschreibung: Natürlichen Logarithmus des Fließkommaregisters FAC berechnen
Einsprungpunkt: $B9EA / 47594
Übergebene Argumente:
Rückgabe-Werte:


Die ROM-Routine LOG[1][2] — manchmal auch als LOGNAT[3] bezeichnet — berechnet den natürlichen Logarithmus der im Fließkommaregister FAC gespeicherten Zahl. Ihr Einsprungpunkt ist in der Tabelle der BASIC-Funktionen an Adresse $A062 hinterlegt, so dass die Routine bei jeder Auswertung der Funktion LOG vom BASIC-Interpreter aufgerufen wird.

Nach dem Aufruf steht in FAC der Wert des Logarithmus, während der Inhalt von ARG undefiniert ist. Wenn LOG mit einer Zahl kleiner oder gleich 0 aufgerufen wird, so löst dies einen ?ILLEGAL QUANTITY ERROR aus.

Neben dem Inhalt der Fließkommaregister FAC und ARG ändert LOG auch den Zähler an Adresse 103/$67, die Hilfszeiger an den Adressen 34/$22 (Low-Byte) und 35/$23 (High-Byte) sowie 113/$71 (Low-Byte) und 114/$72 (High-Byte) und die Fließkommaregister FAC#3 und FAC#4 an den Adressen 87/$57 bis 96/$60.

Algorithmus

LOG führt die Berechnung des natürlichen Logarithmus — des Logarithmus mit der Eulerschen Zahl e = 2.718281828... als Basis — zurück auf den Logarithmus dualis oder Zweierlogarithmus, also den Logarithmus zur Basis 2 (im folgenden mit ld(x) abgekürzt). Dieser ist mit den vom C64 verwendeten Fließkommazahlen besonders einfach zu berechnen. LOG nutzt hierbei die folgende Umformung, wobei der Exponent abzüglich des Exzesses verwendet wird: 

log(FAC) = ld(FAC) × log(2)
         = ld(2Exponent × Mantisse) × log(2)
         = (ld(2Exponent) + ld(Mantisse)) × log(2)
         = (Exponent + ld(Mantisse)) × log(2)

Aus dieser Formel ist ersichtlich, dass LOG lediglich den Zweierlogarithmus für die Mantisse, also für eine Zahl aus dem Intervall [0,5; 1[, zu berechnen braucht. Für alle weiteren Rechenschritte kann LOG auf andere Numerik-Routinen zurückgreifen.

  1. LOG prüft zunächst, ob die Zahl in FAC positiv ist. Wenn dies nicht der Fall ist, so meldet LOG einen ?ILLEGAL QUANTITY ERROR, da der Logarithmus nur für Zahlen größer als 0 definiert ist.
  2. Nun merkt sich LOG den Exponenten von FAC abzüglich des Exzesses auf dem Stack und ersetzt ihn durch die Konstante 128/$80, entsprechend einem Exponenten von 20 = 1. Der Wert von FAC ist damit nur noch durch die Mantisse bestimmt und liegt im Intervall [0.5; 1[.
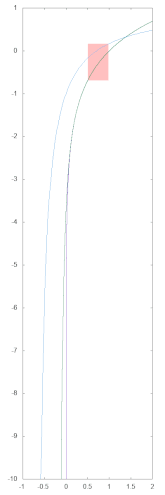
  3. Der Zweierlogarithmus dieser Zahl wird in zwei Schritten berechnet. Zunächst wird der Inhalt von FAC in eine Hilfsfunktion h eingesetzt, deren Schaubild dem des Logarithmus bereits sehr ähnlich ist:
    h(x) = 1 - SRQ(2) / (x + 1/SRQ(2))
    Das Schaubild dieser Funktion ist im nachfolgenden, linken Bild eingezeichnet (blau), zusammen mit dem natürlichen Logarithmus (violett). Die Auswertung von h erfolgt in einzelnen Schritten: Zunächst die Konstante 1/SQR(2) — hinterlegt an Adresse $B9D5 — mittels FADD zu FAC addieren, dann die Konstante SRQ(2) — gespeichert an Adresse $B9DB — mittels FDIV durch FAC dividieren und schließlich das Ergebnis von der Konstanten 1 — zu finden an Adresse $B9BC — mittels FSUB subtrahieren.
  4. Der so erhaltene Zwischenwert wird dann in ein Approximationspolynom 7. Grades eingesetzt, das im Intervall [h(0.5); h(1)[ = [-0.172; 0.172[ den Zweierlogarithmus approximiert:
    p(x) = 0.4342559419 x7 + 0.5765845412 x5 + 0.9618007592 x 3 + 2.885390073 x - 0.5
    Für die Auswertung des Polynoms werden zunächst die Produktterme mittels POLYX ausgewertet und schließlich zum Ergebnis mittels FADD die Konstante -0.5 hinzugezählt. Diese ist im ROM an Adresse $B9E0 hinterlegt.
  5. Zum Wert des Polynoms in FAC wird nun noch der im zweiten Schritt gesicherte Exponent addiert, um den Zweierlogarithmus der ursprünglichen Zahl zu erhalten.
  6. Eine abschließende Multiplikation mit der Konstanten log(2), die im BASIC-ROM an Adresse $B9E5 zu finden ist, ergibt schließlich den gesuchten natürlichen Logarithmus. Da die hierfür benötigte FMULTT-Routine im BASIC-ROM unmittelbar hinter LOG steht, braucht diese nicht mit JSR aufgerufen zu werden, sondern bildet direkt den letzten Schritt der Logarithmus-Berechnung.

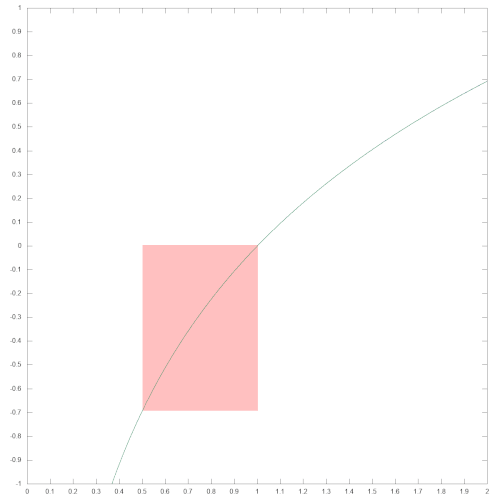
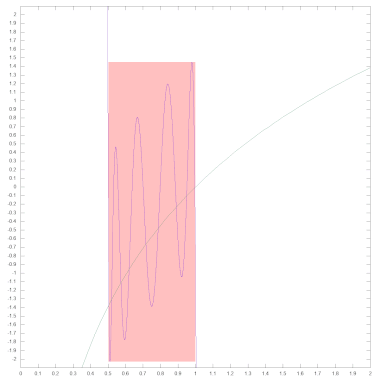
Die folgenden beiden Schaubilder zeigen den Graphen der Approximationspolynoms (grün). In beiden Bildern ist das Intervall, das von der LOG-Routine genutzt wird, hellrot eingefärbt. Zudem ist jeweils der Verlauf der Logarithmus-Funktion (violett), und im linken Bild auch die Hilfsfunktion h(x) (blau) zum Vergleich eingezeichnet. Insbesondere das rechte Bild verdeutlicht, dass das Approximationspolynom auch außerhalb des von LOG genutzten Intervalls [0.5; 1[ eine sehr gute Näherung für den Zweierlogarithmus liefert.

log large.gif
log small.gif


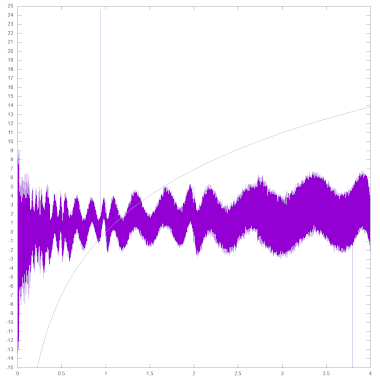
Die nächsten beiden Bilder veranschaulichen noch die Qualität der Approximation. Das linke Bild zeigt im Intervall ]0, 2] die Abweichung zwischen dem Approximationspolynom und dem exakten Logarithmus (violett), multipliziert mit 1010. Diese Werte wurden als doppelt genaue Fließkommazahlen (52 Bit-Mantisse) berechnet. Der maximale Betrag der so ermittelten Abweichung zwischen p(x) und log(x) liegt im von LOG genutzten Intervall [0.5; 1[ bei 2.03E-10. Zum Vergleich ist die Logarithmus-Funktion (grün) in das Schaubild eingezeichnet.

Das rechte Bild zeigt die Abweichung zwischen dem von der LOG-Routine gelieferten Wert und dem exakten Logarithmus (violett, wieder berechnet als Fließkommazahl mit doppelter Genauigkeit). Zur besseren Orientierung ist auch der Verlauf der Logarithmus-Funktion eingezeichnet (grün, in y-Richtung gestreckt um den Faktor 10). Für die Erstellung des Schaubilds wurden die Werte nicht etwa mit PRINT ausgegeben, sondern es wurde der binäre Inhalt von FAC vor und nach dem Aufruf der LOG-Routine ausgelesen. Auf diese Weise gehen keine Ungenauigkeiten oder eventuelle Fehler aus der Umwandlung von der Fließkommadarstellung nach ASCII in die Analyse ein. Zudem wurden als Argumente von LOG nur die ganzzahligen Vielfachen von 2-15 im Intervall ]0; 4] verwendet, um exakt äquidistante Eingabewerte betrachten zu können. Das Schaubild zeigt, dass die Abweichung zwischen Approximationspolynom und exaktem Logarithmus (von durchschnittlich 0.82E-10, maximal 2.03E-10) deutlich kleiner ist als die durch Rundungsfehler verursachten Differenzen (von durchschnittlich 1.78E-10, maximal 12.98E-10, mit einzelnen Ausreißern von bis zu 114.14E-10 aufgrund eines Fehlers in der Multiplikationsroutine).

log double error.gif
log real error.gif


Laufzeitverhalten

Falls nicht bereits bei der Bereichsprüfung zu Beginn des Algorithmus ein Fehler gemeldet wird, so führt LOG in jedem Fall alle Berechnungsschritte durch.

Da die in POLYX genutzten ROM-Routinen FADD und FMULT allerdings auf einen Summanden bzw. einen Faktor von 0 prüfen und in diesem Fall keine Addition bzw. Multiplikation durchführen, verkürzt sich die Laufzeit deutlich, sofern die in Schritt 3 des Algorithmus berechnete Hilfsfunktion h(x) den Wert 0 zurückliefert. Dies ist genau dann der Fall, wenn sich x als Produkt aus einer Zweierpotenz und der Konstanten 1 / SQR(2) schreiben lässt. In diesem Sonderfall beträgt die Laufzeit von LOG zwischen 5635 Takten für x = 1 / SQR(2) und 6185 Takten für x = 2-127 / SQR(2).

In allen anderen Fällen ist aufgrund der großen Zahl von Rechenoperationen kein funktionaler Zusammenhang zwischen der in FAC übergebenen Zahl und der Laufzeit von LOG erkennbar. Beim Sonderfall log(1) = 0 beträgt die Laufzeit 17913 Systemtakte, ansonsten lag die Rechenzeit im Rahmen ausgiebiger Messreihen zwischen 17933 und 21973 Systemtakten.

Ein Systemtakt entspricht auf dem Commodore 64 rund einer Mikrosekunde (μs). Im ungünstigsten Fall benötigt die LOG-Routine also etwa 22 Millisekunden (ms).

Bugs

  • Wie aus dem obigen Schaubild mit den Abweichungen zwischen dem Ergebnis von LOG und dem exakten Logarithmus ersichtlich, zeigen sich die Auswirkungen eines Fehlers in FMULT auch in den Ergebnissen der hierauf aufbauenden ROM-Routine LOG: Bei insgesamt 5 von 131072 Berechnungen der Analyse verursachte dieser Fehler eine Abweichung von mehr als 13E-10, im Extremfall — bei der Berechnung von LOG(124453 / 32768) — sogar von 114.14E-10.

Weblinks

Quellen

  1. ↑ Florian Müller: C64 für Insider, S. 462
  2. ↑ Said Baloui/Rolf Brückmann/Lothar Englisch/Jacques Felt/Ralf Gelfand/Klaus Gerits/Darko Krsnik: Das neue Commodore 64 Intern Buch, S. 633
  3. ↑ Winfried Kassera/Frank Kassera: C64 Programmieren in Maschinensprache, S. 300
Abgerufen von „https://www.c64-wiki.de/index.php?title=LOG_(ROM-Routine)&oldid=236639“