Elementarmathematik vom algorithmischen Standpunkt

Elementarmathematik vom algorithmischen Standpunkt
	Sprache	deutsch
	Autor(en)	Arthur Engel
	Verlag	Ernst Klett Stuttgart
	Jahr	1977, 1. Aufl.
	ISBN	ISBN 3-12-983340-4
	Neupreis	22,00 DM bzw. 27,00 DM je nach Erscheinungsjahr 1977 bzw. 1981
	Datenträger
	Seitenzahl	222
	letzte Auflage	1977
	Genre	Programmieren
	Information	Klett-Studienbücher Mathematik

Beschreibung

"Schwerpunkt des Buches ist die Algorithmik. Zugleich ist es ein vielseitiges Mathematikbuch, das die mathematischen Kenntnisse des Lesers erweitern und vertiefen möchte. Als Nebenprodukt erwirbt der Leser die Kunst des Programmierens. ...

Das Buch ist aus einem Seminar über computerorientierte Mathematik hervorgegangen, das regelmäßig an der Universität Frankfurt angeboten wurde."
(aus dem Vorwort)

Der Aufbau der Beispielprogramme wird durch Ablaufdiagramme oder Flußdiagramme erklärt. Der Programmcode ist in BASIC geschrieben und kann daher mit den meisten Heimcomputern direkt oder ggf. leicht angepasst ausgeführt werden.

Inhaltsverzeichnis

Vorwort


1. Algorithmen
1.1.   Algorithmen und Programme
1.2.   Das 3A+1-Problem. Empirische Untersuchung eines Algorithmus
1.3.   Algorithmische Definition einiger Funktionen
1.3.1. Die Maximum- und die Minimum-Funktion
1.3.2. Fakultät und Potenz
1.3.3. Die Funktion "Ganzer Teil"
1.3.4. Wurzelfunktionen
1.3.5. Logarithmen, Zufallsziffern und Potenzen
1.3.6. Zufallsgeneratoren
1.4.   Die Fibonacci-Folge

2. Zahlentheorie
2.1.   Umwandlung vom 10-System ins b-System und umgekehrt
2.2.   Euklidischer Algorithmus
2.3.*  Eine Erweiterung des euklidischen Algorithmus
2.4.   Primzahlen
2.5.   Periodische Dezimalzahlen
2.6.   Kettenbrüche
2.7.*  Chinesische Primzahlen
   
3. Geometrie
3.1.   Die Quadratur der Parabel nach Archimedes
3.2.   Die Berechnung von π nach Archimedes
3.3.   Algorithmen für die trigonometrischen Funktionen
3.4.   Die Methode von Cusanus
3.5.   Die Quadratur der Hyperbel
3.6.   Konvergenzbeschleunigung. Das Romberg-Schema
3.7.   Gitterpunkte im Kreis (π durch Zählen)
3.8.   Die Leibniz-Reihe für π
3.9.   Monte-Carlo-Methode zur Bestimmung von π

4. Numerische Mathematik
4.1.   Lösung einer Gleichung
4.2.   Das Maximum einer unimodalen Funktion
4.3.   Numerische Integration
4.3.1. Trapezregel, Mittelwertregel und Simpson-Regel
4.3.2. Das Romberg-Verfahren
4.3.3. Beweis der Simpson-Regel und der Hermite-Regel
4.4.   Differentialgleichungen
4.4.1. Wachstum, Zerfall und Schwingung
4.4.2. Numerische Integration von Differentialgleichungen
4.4.3. Simulation dynamischer Prozesse
4.5.   Die harmonische Reihe
4.6.   Die Berechnung von e auf 250 Stellen

5. Kombinatorik und Wahrscheinlichkeit
5.1.   Programme für das Pascal-Dreieck
5.2.   Frequenzzählungen
5.3.   Permutationen
5.4.   Wahrscheinlichkeitsprobleme

 6. Simulation von Zufallsprozessen
6.1.   Der Zufallsgenerator
6.2.   Simulation mit dem Zufallsgenerator
6.3.   Simulation ohne Zufallsgenerator

7. Sortieren

8. Das Acht-Damen-Problem

9. Lösungen der Aufgaben

Literaturverzeichnis

Register

Leseproben

1) Aus dem Kapitel 2. Zahlentheorie

2.4. Primzahlen

Eine natürliche Zahl heißt Primzahl, wenn sie genau zwei Teiler hat. Schon Euklid (365? − 300?) wußte, daß es unendlich viele Primzahlen gibt.
Die Primzahlfolge  2, 3, 5, 7, 11, 13, 17, 19, 23, . . . ist sehr unregelmäßig.
Einerseits gibt es beliebig große Primzahllücken. Z.B., n! + 2, n! + 3, . . . , n! + n sind  n - 1  aufeinanderfolgende zusammengesetzte Zahlen. Andererseits gibt es höchstwahrscheinlich unendlich viele Primzahlzwillinge, d.h. Primzahlpaare der Form (p, p + 2).
Jede Primzahl  > 3  hat die Form  6 n − 1  oder  6 n + 1,  da für n ≥ 1 Zahlen der Form  6 n, 6 n ± 2, 6 n + 3  offensichtlich keine Primzahlen sind. Deshalb haben alle Primzahlzwillinge außer  (3, 5)  die Form  (6 n − 1, 6 n + 1).
Ist  n > 1  keine Primzahl, dann kann man sie nichttrivial zerlegen:

n = d₁ ∙ d₂,    1 < d₁ < n,  1 < d₂ < n

Die Teiler  d₁  und  d₂  können nicht beide  > √ ̅n sein, sonst wäre d₁d₂ > n.
Eine Nichtprimzahl  n  hat also einen nichttrivialen Teiler  d ≤ √ ̅n.  Mit anderen Worten: Hat n  keinen Teiler d in  1 < d ≤ √ ̅n,  dann ist  n  eine Primzahl.
Wir wollen eine Primzahltafel herstellen. Alle einschlägigen Verfahren beruhen auf Division oder Siebung.

Primzahltafel durch Division
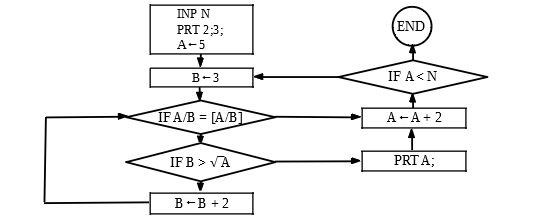
Wir wollen alle Primzahlen ≤ N  drucken. Die Primzahlen 2 und 3 spielen eine Son- derrolle und werden am besten gesondert gedruckt. Es sei  A  die zu testende Zahl und  B  sei der Testteiler. Anfangs ist  A = 5  und B = 3. Wir müssen  A  durch alle Primzahlen  ≤ √ ̅A  teilen. Geht eine Division auf, so ist A keine Primzahl. Andern- falls ist  A  eine Primzahl und wird gedruckt. Danach wird  A ← A + 2,  B ← 3 gesetzt und der Zyklus wiederholt sich. Der Testteiler B braucht nur die Primzahlen ≤ √ ̅A  zu durchlaufen. Da es unbequem ist, die Primzahlen  ≤ √ ̅N zu speichern, lassen wir B alle ungeraden Zahlen  ≤ √ ̅A  durchlaufen. Fig. 2.13 zeigt das Fluß- diagramm und das BASIC-Programm für N = 1000.

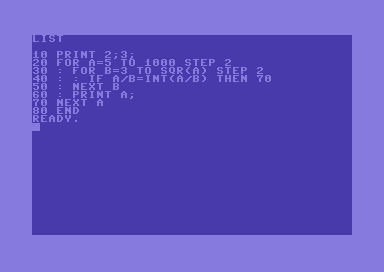
            10 PRINT 2;3;   
            20 FOR A = 5 TO 1000 STEP 2
            30     FOR B = 3 TO SQR(A) STEP 2
            40         IF A/B = INT(A/B) THEN 70
            50     NEXT B
            60     PRINT A;
            70 NEXT A
            80 END

2  3  5  7  11  13   7  19 23 29 31 37 41 43 47 53 59 61 67 71 97 79 83 89 97 101
103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 351 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 673 677 683 671 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997

Fig. 2.13

Aufgaben:

1. Bei jeder Ausführung der Zeile 40 wird links und rechts vom Gleichheitsszeichen   dividiert. Man braucht nur einmal zu dividieren, falls man 40 durch die beiden

40 C = A/B           45 IF C = INT(C)

 ersetzt. Vergleiche die Rechenzeiten des alten mit dem so modifiziertem Programm  für N = 2000. Entferne vorher aus beiden Programmen die Druckanweisungen.

2. Schreibe ein Programm, das die Anzahl der Primzahlen im Intervall von M bis N  zählt (M > 3 und ungerade). Wieviel Primzahlen gibt es zwischen 1000 und 2000,  2000 und 3000, 3000 und 4000, 10000 und 11000?

2) Aus dem Kapitel 6.2. Simulationen mit dem Zufallsgenerator

3. Beispiel: Das Crap-Spiel
Das Crap-Spiel ist das schnellste und populärste amerikanische Würfelspiel. Die Spiel- regen lauten:

1. Rolle zwei Würfel und bestimme die Augensumme S. S = 7 oder S = 11 gewinnt
    sofort. S = 2 oder S = 2 oder S = 12 verliert sofort.
2. Bei jeder anderen Summe nennt man diese Summe den "Punkt" P und spielt so
    lange weiter, bis entweder S = 7 (ein Verlust) oder S = P (ein Gewinn) erscheint.

         10 READ N,G,W   
         20 FOR I=1 TO N
         30     S=INT(6*RND)+INT(6*RND)+ 2
         40     W= W+1
         50     IF S=7 OR S=11 THEN 120
         60     IF S=2 OR S=3 OR S=12 THEN 130
         70     P=S
         80     S=INT(6*RND)+INT(6*RND)+2
         90     W=W+2
        100     IF S<>7 AND S<>P THEN 80
        110     IF S=7 THEN 130
        120     G=G+1
        130 NEXT I
        140 PRINT "SPIELE="N,"GEWINNE="G,"VERLUSTE="N-G,"WÜRFE="W
        150 DATA 1000,0,0
        160 END 

        Fig. 6.10

Wir wiederholen das Spiel n-mal und schätzen die Gewinnwahrscheinlichkeit sowie die mittlere Spieldauer (Wurfzahl).   Der Befehl  INT(6*RND)+1  liefert einen Wurf eines Würfels.  Daher ist  INT(6*RND)+INT(6*RND)+2  die Augensumme zweier Würfe. Die Variablen C und W zählen die Gewinne bzw. die Doppelwürfe. Das Pro- gramm in Fig. 6.10 dürfte ohne Kommentar verständlich sein.

C64 - Beispiele

Das Primzahl-Programm auf dem C64

• 

  Listing

• 

  Ausgabe

Das Crap-Spiel-Programm auf dem C64

Das Programm wurde für den C64 leicht modifiziert:

• Funktion RND() in Zeile 30 und 80
• Anzeige des aktuellen Wurfes in der zusätzlichen Zeile 35
• "WUERFE" statt "WÜRFE" in Zeile 140
• Anzahl der Würfe nur 100 statt 1000 (Daten in Zeile 150)

• 

  Listing

• 

  Ausgabe (nur Summen von Zeile 140)

Meinung

Petrus: "Ein sehr inhaltsreiches Lehrbuch, das trotz seines Alters immer noch interessant ist. Zum Verständis der meisten Kapitel sind einige mathematische Kenntnisse erforderlich. Die Programme sind kurz und daher bequem abzutippen. Für alle, die an mathematischen Algorithmen interessiert sind, ist dieses Buch eine Fundgrube."

Weblinks

• Katalog der Deutschen Nationalbibliothek: 3-12-983340-4

Wikipedia: Arthur Engel