Bitmap

Als Bitmap wird ein Speicherbereich bezeichnet, in dem festgehalten ist, ob in einer zugehörigen Grafik ein Punkt (Pixel) gesetzt ist oder nicht.

Die Bitmap des C64

Der C64 besitzt zwei Bitmap-Modi.

• Im Hires Bitmap-Modus wird ein Pixel durch ein 1-Bit repräsentiert, ein nicht gesetztes Pixel entsprechend folglich durch ein 0-Bit.
• Im Multicolor Bitmap-Modus wird ein Pixel durch zwei Bits definiert, wobei es vier verschiedene Möglichkeiten gibt: 00, 01, 10 und 11.

Eine komplette Bitmap besitzt 320×200 Bits, ist also 8000 Bytes lang.

Jede Grafik, egal in welchem Modus sie angezeigt wird, enthält (zumindest) eine Bitmap. Im Bitmap-Modus kann im Gegensatz zum Textmodus direkt auf die einzelnen Pixel zugegriffen werden.

Bitmap-Format

Wollte man jedem Punkt eine von den 16 möglichen Farben geben, würde jedes Pixel 4 Bits und damit die Bitmap 32.000 Bytes benötigen. Da dies bei dem begrenzten Speicher nicht möglich ist, haben die Entwickler eine Architektur für den Bitmap-Modus gewählt, die der des Textmodus ähnlich ist.

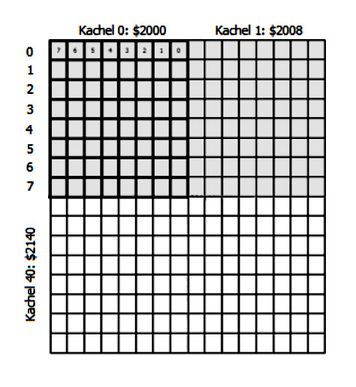
Die Pixel der Bitmap sind nicht linear angeordnet, sondern in 8x8 Pixel großen Kacheln, wie die Zeichen im Zeichensatz. In einer 320 Pixel langen Zeile liegen so 40 Kacheln, in einer 200 Pixel langen Spalte 25 Kacheln, wodurch die Bitmap-Bytes in 40×25 Kacheln angeordnet sind.

Reihenfolge der Bytes in einer Bitmap (S = Spalte, Z = Zeile):

   S      0        1                                 39
  \  +--------+--------+-- ...		  ... --+--------+
 Z   |    0   |    8   |      		        |   312  |
     |    1   |    9   |      		        |   313  |
     |    2   |   10   |      		        |   314  |
   0 |    3   |   11   |      		        |   315  |
     |    4   |   12   |      		        |   316  |
     |    5   |   13   |      		        |   317  |
     |    6   |   14   |      		        |   318  |
     |    7   |   15   |      		        |   319  |
     +--------+--------+-- ...		  ... --+--------+
     |   320  |   328  |      		        |   632  |
     |   321  |   329  |      		        |   633  |
     |   322  |   330  |      		        |   634  |
   1 |   323  |   331  |      		        |   635  |
     |   324  |   332  |      		        |   636  |
     |   325  |   333  |      		        |   637  |
     |   326  |   334  |      		        |   638  |
     |   327  |   335  |      		        |   639  |
     +--------+--------+-- ...		  ... --+--------+
     |                                             	 |
     .        .        .                        .        .
     .        .        .                        .        .
     .        .        .                        .        .
     |                                                   |
     +--------+--------+-- ...		  ... --+--------+
     |  7680  |  7688  |      		        |  7992  |
     |  7681  |  7689  |      		        |  7993  |
     |  7682  |  7690  |      		        |  7994  |
  24 |  7683  |  7691  |      		        |  7995  |
     |  7684  |  7692  |      		        |  7996  |
     |  7685  |  7693  |      		        |  7997  |
     |  7686  |  7694  |      		        |  7998  |
     |  7687  |  7695  |      		        |  7999  |
     +--------+--------+-- ...		  ... --+--------+

Farben

Die Bitmap enhält keine Farben, ist also attributlos (monochrom). Zum Anzeigen der Bitmap-Grafik ist es aber erforderlich, Farben zur Verfügung zu stellen. Der Benutzer kann diese frei wählen. Damit man die Bitmap gut erkennen kann, sollte jedem Bit- bzw. Doppelbit-Wert eine Farbe zugeordnet werden, die für alle Kacheln gleich ist.

Will man im Hires Bitmap-Modus eine Darstellung "Weiß auf Blau" wählen, so müssen die 1000 Bytes des Video-RAMs mit dem Byte 16*1+6 ($16) gefüllt werden. Beispiel: Bild:Hi-Eddi-ALU1.gif

Im Multicolor Bitmap-Modus kann man eine Graustufen-Darstellung wählen mit 16*11+12 ($BC) für das Video-RAM (Bits %10 und %01), 15 ($0F) für das Farb-RAM (Bits %11) und 0 als Hintergrundfarbe (Bits %00). Beispiel: Bild:Apfelmann 4f.png.

Berechnung eines Punktes

Im Hires Bitmap-Modus wird ein Punkt in der Bitmap auf folgende Weise berechnet:

Der Anfang des Grafikspeichers

Eine Adresse x,y errechnet sich nun folgendermaßen (⇒ Beispiel: x = 100, y = 50, Grafikspeicher ab 8192): Offset der zugehörigen Kachel im Grafikspeicher: k = INT(x/8)*8 + INT(y/8) * 320 INT(x/8)*8 bewirkt, dass die niederwertigsten 3 Bits des x-Wertes gelöscht werden (das ist der nächstniedrige ganzzahlig durch 8 teilbare Wert, ein alternativer Term hierfür siehe unter Anwendung in BASIC V2). Diese 3 Bits der Pixelzeile werden dann weiter unten benötigt. ⇒ Beispiel: k = 96 + 1920 = 2016 Offset des Bytes in dieser Kachel (0 bis 7): pz = (y AND 7) Das "AND" belässt hier als bit-orientierte Operation die niederwertigsten 3 Bits des y-Wertes. Die Maske ist die Summe der Bit-Wertigkeiten von Bit 0 bis Bit 2 (1+2+4). ⇒ Beispiel: pz = 2 Wert des angepeilten Bits in diesem Byte: px = 2↑(7 - (x AND 7)) Das "AND" belässt hier als bit-orientiere Operation die niederwertigsten 3 Bits des x-Wertes. Die Maske ist die Summe der Bit-Wertigkeiten von Bit 0 bis Bit 2 (1+2+4). ⇒ Beispiel: px = 8 (das ist das vierte Bit von rechts, Bit 3) Byte-Adresse: ba = 8192+k+pz Pixel setzen: POKE ba, PEEK(ba) OR px Pixel löschen: POKE ba, PEEK(ba) AND NOT px Beispiel für Pixel setzen und löschen: POKE 10210, PEEK(10210) OR 8 POKE 10210, PEEK(10210) AND NOT 8

Anwendung in BASIC V2

Grafikverwendung nur mit Mitteln des BASIC V2.
Zur Beschleunigung werden

• in Z() die Kachelzeilenadressen
• in B() die Bit-Werte für eine Pixelzeile einer Kachel

vorberechnet.
Die Grafik wird liegt ab Adresse 8192 ($2000), die Farbinformationen im Bildschirmspeicher ab 1024 ($0400).
Mit Hilfe eines temporär angelegten Integer-Arrays A%(), das von BASIC mit Wert 0 initialisiert wird, erfolgt indirekt das Löschen der Bitmap, da das Array unmittelbar auf das Programm im Speicher folgt und rund 16000 Bytes belegt und damit den Speicher der Bitmap abdeckt.

100 REM --- INITIALISIERUNG ---
105 REM BITMAP MIT INTEGER-ARRAY LOESCHEN
110 DIM A%(8000): CLR
120 REM ARRAYS FUER PIXELZEILENMASKE, ZEILENANFANGSADRESSEN
130 DIM B(7),Z(24)
140 REM PIXELZEILENMASKENWERTE BERECHNEN
150 W=1: FOR I=7 TO 0 STEP -1: B(I)=W: W=W+W: NEXT
160 REM ZEILENANFANGSADRESSEN BERECHNEN
170 FOR I=0 TO 24: Z(I)=8192+320*I: NEXT
180 REM GRAFIKMODUS EIN, RAHMENFARBE GRAU
190 POKE 53265,59: POKE 53272,24: POKE 53280,15
200 REM ZEICHENFARBE, HINTERGRUND DER BITMAP: HELLGRUEN/SCHWARZ
210 F=13*16+0: FOR I=1024 TO 2023: POKEI,F: NEXT
215 REM --- ZEICHNEN ---
220 REM PUNKTIERTE LINIE ZEICHNEN
230 FOR X=0 TO 99: Y=X+X
240 REM PIXEL SETZEN
250 GOSUB 320
260 NEXT
270 REM AUF TASTE WARTEN
280 WAIT 198,1
285 REM --- GRAFIK AUSSCHALTEN ---
290 PRINT CHR$(147)
300 POKE 53265,155: POKE 53272,21
310 END
315 REM --- SUB PIXELSETZEN ---
320 G=Z(Y/8) + (X AND 504) + (Y AND 7): POKE G, PEEK(G) OR B(X AND 7): RETURN

Das "AND 504" löscht hier als bit-orientiere Operation die niederwertigsten 3 Bits des x-Wertes, entspricht also dem INT(x/8)*8. Die Maske ist die Summe der Bit-Wertigkeiten von Bit 3 bis Bit 8 (8+16+32+64+128+256).

Verwandte Themen

• Bitmap-Modus
• Hires Bitmap-Modus
• Multicolor Bitmap-Modus